932. Beautiful Array

#Algorithm #Algorithm-Divide_N_Conquer

932. Beautiful Array

1. 문제

1-1. 원문

An array nums of length n is beautiful if:

Given the integer n, return any beautiful array nums of length n. There will be at least one valid answer for the given n.

Example 1:
Input: n = 4
Output: [2,1,4,3]

Example 2:
Input: n = 5
Output: [3,1,2,5,4]

Constraints:

1-2. 내용 번역

길이가 N인 배열이 있고, 이 배열은 조건에 맞아야 한다.

2. 문제 이해

2-1. 내용 이해

배열 길이가 N이라고 할 때, 원소값이 1,2,...,N인 배열을 리턴해야 한다.

인덱스의 원소값 조건 문장은 예제로 이해하는 것이 필요했음
nums[5]*2 != nums[4] + nums[6] 이기도 하고,
nums[5]*2 != nums[1] + nums[6] 이기도 하다.

2-2. 접근법 생각

Topic의 태그가 Divide & Conquer 이였다.
양 옆의 합이 가운데의 2배가 아니면 된다.
...
무작위로 나열하고 확인하는 방식을 사용해볼까? constraint가 1000이라고 했으니 가능하지 않을까?
-> 시간복잡도 측정 불가를 넘어 랜덤발생기의 촉을 믿는 방법이다.
...
중간 수를 2배하면 뭐든 짝수가 될테니 양쪽의 합은 홀수면 되나?
-> [1,2,3,4,5]를 예시로 사용하면 [1,3,2,4,5] 이렇게?
-> 이걸보니 한 칸씩 건너뛴 수들은 짝수 + 홀수 페어네? 좀 더 큰 수로 해볼까?
[1,2,3,4,5,6,7,8]를 예시로 사용하면 [1,3,2,4,5,7,8]
--> 아맞다. 바로 이어진 3개 수가 아니라 띄엄띄엄 떨어진 수에도 적용해야지.. 4*2=3+5니까 안되겠네...
...
풀이를 보자..!

2-3. 적용한 풀이

Java | Clear Thinking Process - Divide and Conquer :: WelchJ
접근 프로세스를 설명하고 있어서 나의 접근방식과 비교하게 되었고, 어떤 부분에서 더 심화시켰는지 확인하고 배울 수 있는 풀이였다. (나의 이해 흐름을 서술했기 때문에 나의 풀이는 위의 링크의 보충설명 정도로 생각하고, 명확한 풀이는 위의 링크를 참고하자.)

WelchJ의 풀이에서는 k인덱스의 원소 값 * 2 != i인덱스의 원소값 + j인덱스의 원소값 이 조건을 distance의 개념으로 생각하면서 논리가 전개된다.
num[k]*2 == num[i] + num[j] 를 다음의 식 num[k]-num[i] == num[j]-num[k] (i<k<j, num[i] < num[k] < num[j])으로 생각해보면 이것은 k와 i, j 각각의 거리이다.
즉, 사이의 거리가 같으면 공식이 성립하므로 조건에 부합하지 않는다.

거리를 다르게 하기 위해서는 아래의 그림을 생각해 볼 필요가 있다.
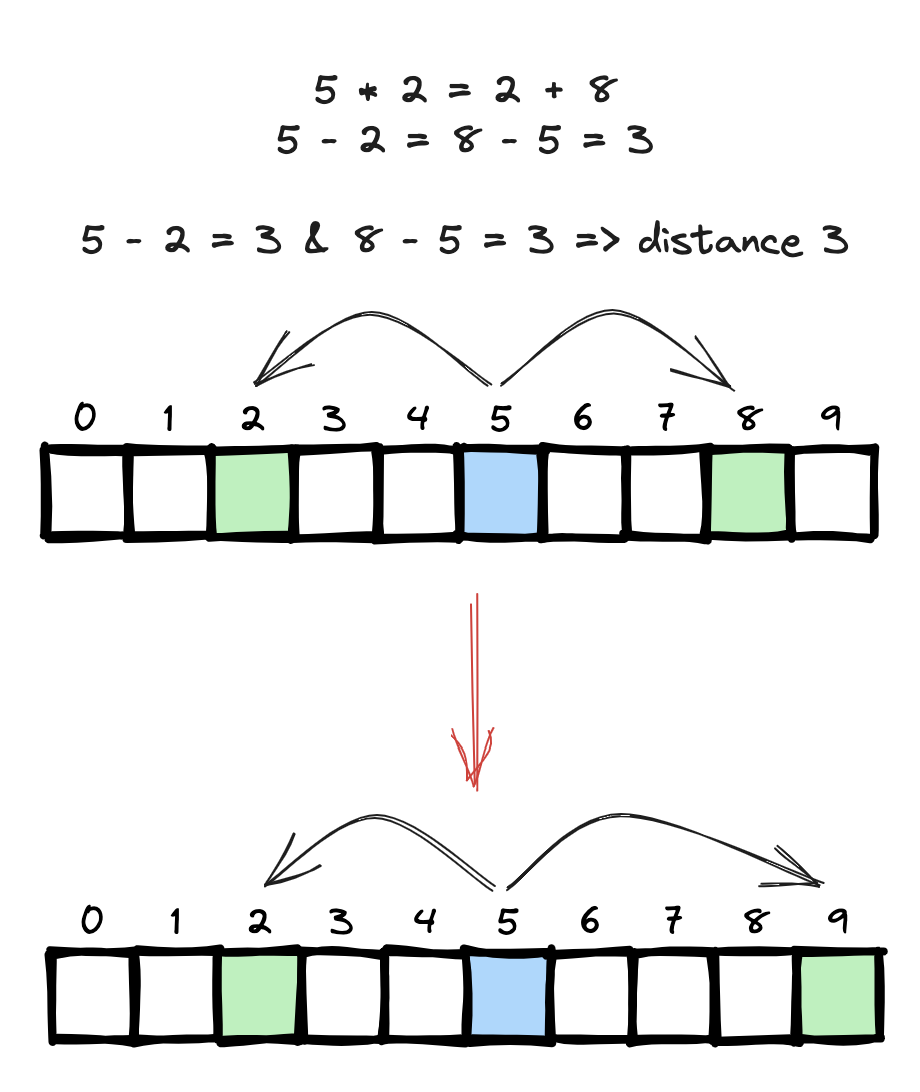
932_beautiful_array.png|400
거리가 달라지면 조건이 부합되는걸 볼 수 있다. 거리를 다르게 한다는 말은 위의 그림은 인덱스의 관점으로 바라보았지만, 인덱스 엘리먼트의 값의 관점에서도 동일하게 적용할 수 있기 때문에 관점의 이동이 필요하다.

이제 여기에서 거리를 다르게만 만들면 될 것 같다. 그런데 이것은 알고리즘이고, 어떤 규칙이 꼭 있어야 하니까 기준을 만들어줘야 한다. 같은 거리의 인덱스, 그것들이 가지고 있는 각각의 엘리먼트의 거리는 달라야한다. 여기서 하나의 규칙을 더 찾아야 하는데, 같은 거리의 인덱스의 숫자를 보자. 두 수가 모두 홀수 혹은 짝수이다. 그럼 하나는 홀수, 하나는 짝수로 고르게 하는것을 기준으로 삼자(1).
*(1) 위에서도 홀수와 짝수를 가장 처음 생각하기는 했지만, 홀수와 짝수를 거리를 다르게하기 위한 기준이 된다는것으로 이어지지 않았다.

그럼 이제 num[i], num[j]는 각각 모두 홀수, 모두 짝수가 되어야 한다. 그리고 num[k]는 num[i] or num[j] 편 중 하나에 속한 어떤 엘리먼트일 것이다. 그럼 여기서 그룹이라는 개념이 나오게 된다.
[1, 3, 5, 7, 9], [2, 4, 6, 8, 10].
9를 num[k]로 선택하면 num[i]는 num[k]와의 거리가 모두 짝수가 되고, num[j]는 모두 홀수가 되기 때문에 모든 조건에 부합한다.
하지만 각각의 그룹 안에서는 여전히 동일한 거리가 나올 수 있다.

위의 과정을 조금 더 깊게 보면 맨 처음 배열의 거리는 1+1*0, 1+1*1, 1+1*2, ... 이다.
둘로 나눈 배열의 거리는 2+2*0, 2+2*1, 2+2*2,... 이다.
곱해지는 수를 보면 해당 거리는 0, 1, 2로 처음과 똑같이 구분되는것을 알 수 있다. 그렇다면 나눈 배열에도 위의 조건을 동일하게 적용하자(2).
*(2) 0, 1, 2가 거리적인 의미에서 차이를 보완할 수 없게 만든다는 것을 이해하는데에 시간이 오래 걸렸다.

이렇게 되면 일반적인 분할 조건, 정렬 조건이 모두 나왔다. 이것을 구현하면 된다.

3. 구현

//O(nlogn)

class Solution {
    fun beautifulArray(n: Int): IntArray {
        val nums = IntArray(n)

        for(i in 0..n-1) {
            nums[i] = i+1
        }

        return dnq(nums)
    }

    fun dnq(nums: IntArray): IntArray {
        if (nums.size ==1) return nums

        //n == 7 -> 0, 1, 2, 3, 4, 5, 6
        val rightSize = nums.size/2
        val leftNums = IntArray(nums.size-rightSize) //leftSize == 4
        val rightNums = IntArray(rightSize) //rightSize == 3

        var idx = 0
        while(idx < leftNums.size) { // 0, 1, 2, 3
            leftNums[idx] = nums[idx*2] //0, 2, 4, 6
            idx++
        }

        idx = 0
        while(idx < rightNums.size) { //0, 1, 2
            rightNums[idx] = nums[idx*2+1] //1, 3, 5
            idx++
        }

        return dnq(leftNums) + dnq(rightNums)
    }
}